The street crossing puzzle

I've been thinking a lot recently about how to cross the street. Specifically, when standing at the position labeled START in the map shown here, what's the best way to get to the position labeled HOME?

There are two main strategies that I know some people employ:

Disregarding: Never cross at the first vertical crosswalk. Instead, always proceed to the second crosswalk.
Opportunism: If the first vertical crosswalk is available when you arrive, cross there. Otherwise, proceed to the second crosswalk.

Interestingly, I asked around and found that both Disregarding and Opportunism are popular strategies — and that advocates of one consider their own strategy to be obviously superior:

Disregarder: “By proceeding to the second crossing, you can cross in whichever direction is available, then cross in the other direction immediately afterwards. It's more efficient if you don't have to wait for the right direction to become available.”

Opportunist: “By crossing immediately, you take the opportunity to bring yourself closer to your goal right away; it's more efficient if you have to wait for only one light rather than two.”

I decided to find an analytic solution, which led to some beautiful graphs— and an unexpected verdict.

(Which strategy do you think is better? Are they equally efficient?)

The crosswalk model

Here are some of the main features of my model:

Each crosswalk switches between horizontal and vertical with a cycle time of S seconds.
You take a constant amount of time T seconds to cross any street. (For example, you don't sprint to make it across the street in time.)
You take less than one cycle time to cross the street. 0<T<S
At the second crosswalk, there is no "dead time" where no one can walk. (In practice, dead time would be used to allow cars to make turns against the direction of traffic.)
The first and second crosswalk have independent cycles.

Depictions of crossing strategies

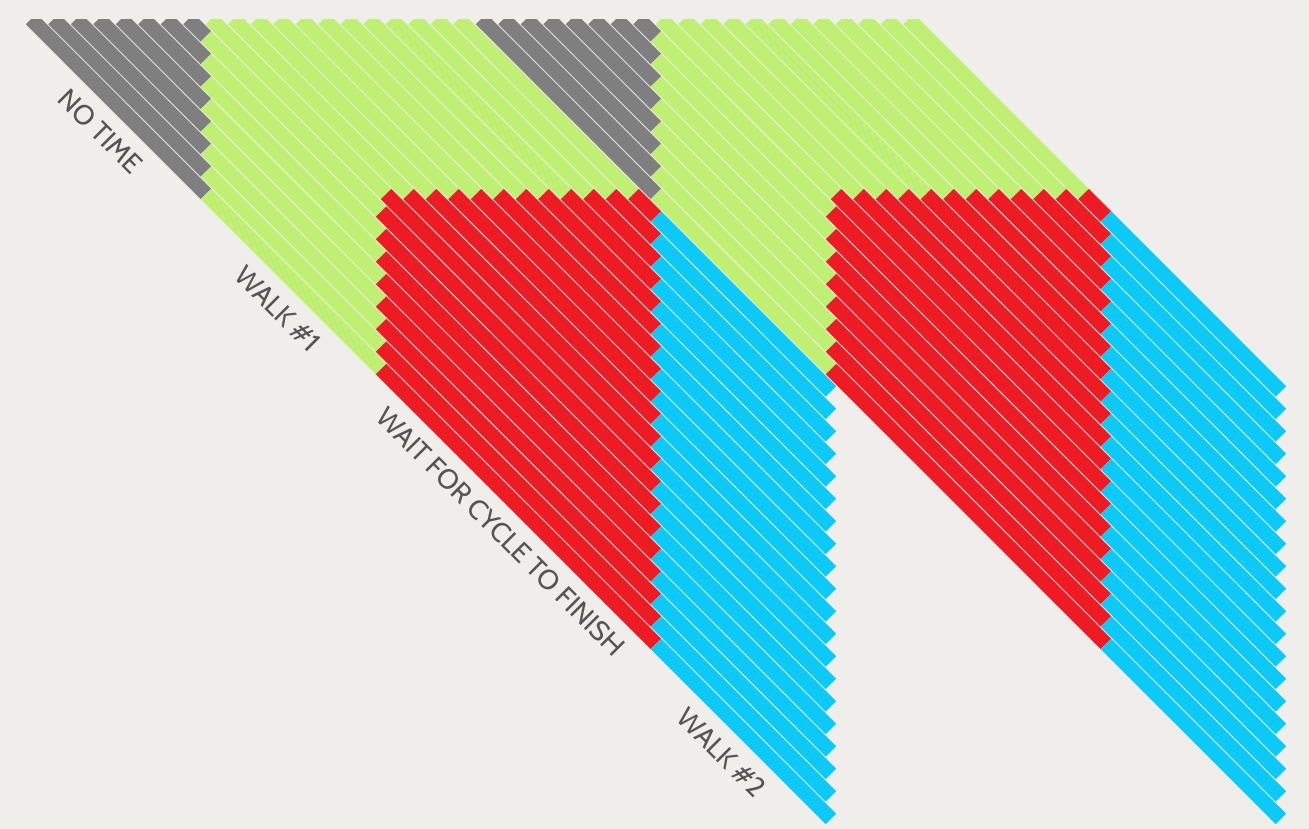
When you wait to cross the street both directions

In this image, you see all possible outcomes of crossing the street twice consecutively. The horizontal axis records the state of the crosswalk, which alternates between allowing horizontal and vertical crossings. The vertical axis measures the activity of a person over time — the person's arrival is marked at the top of the image, and time proceeds downward. As the person's time advances, so does the state of the crosswalk — so individuals are represented by lines at a 45° angle.

Each diagonal line represents a single individual who has arrived at the crosswalk when it's in a particular state. As the person waits and walks, their line changes color. For example, the leftmost line in the image represents the worst case scenario: the person arrives having not enough time to cross, and so must wait (grey segment). When the light changes, the person crosses (green segment). Afterwards, the person waits for the current cycle to finish (red segment) so as to cross in the other direction next (blue segment).

Here are some interesting observations about waiting times in this scenario:

The grey region has width and height equal to your crossing time T, because you only miss the light if it has fewer than T seconds remaining.
The image is periodic in the horizontal direction with period S, because the state of the crosswalk is periodic.
The red region has a 90° corner because if you must wait for a new cycle to begin, you'll spend T seconds walking across, and the full remainder of the cycle S−T seconds waiting for the light to change. On the other hand, if you arrive after the cycle has started, you'll spend T seconds walking across, and less than the full cycle waiting.
(!) The waiting-time regions (red and grey) align perfectly, forming triangular regions of width and height S. This is because the first waiting time is at worst T, and the second waiting time is at worst S−T.
As a corollary, average waiting time in the second crossing strategy is independent of walking speed; the gain from crossing the street quickly is cancelled by the fact that you'll have to wait that much longer for the cycle to complete once you've reached the other side.

When you must cross the street in only one direction

In the case where you can't cross at the first crosswalk, the Opportunist and the Disregarder follow the same strategy: they proceed to the second crosswalk and cross as efficiently as possible.

So, if there is to be any difference in waiting times between the two strategies, it must appear when it's genuinely possible to cross the street — when the Opportunist chooses to cross, and the Disregarder chooses not to.

In that case, the Opportunist can cross in one direction immediately, spending no time waiting at all. Then, at the second crosswalk, the Opportunist's outcomes look like this:

The worst case scenario is when the Opportunist arrives during the tail end of the cycle which they need to take — they have no time to cross, and must wait for one complete cycle in the wrong direction before they can cross. The best case, occurring prevalently, is when they arrive sometime during the cycle which they need to take and hence wait no time at all to cross the second time.

The waiting time area for the Opportunist is sum of the areas of the red and grey regions; they form a triangle of width S+T.

Average waiting time

Here, we'll compute the average waiting time of each strategy to get a better feel for the difference.

The waiting time area for a Disregarder is S2. The waiting time area for an Opportunist depends on whether they were able to cross at the first crosswalk or not: if they were able, the waiting time area is 12(S+T)2, the area of the triangle in the previous section. If they weren't able to cross at the first crosswalk, they behave like a Disregarder would, with a waiting time area of S2.

How often will the Opportunist be able to cross at the first crosswalk? The crosswalk has a period of length 2S. S of those seconds are uncrossable because the light is in the wrong direction; T of those seconds are uncrossable because there isn't enough time to cross even though the light is in the right direction. The rest of the time, the Opportunist can cross. That's S−T out of 2S.

The average waiting time occurs when we divide the waiting-area by the period 2S. Thus the Disregarder's average waiting time is \(\)

S22S=S/2,half of a cycle. The Opportunist's average waiting time is a weighted average:12S⎡⎣⎢⎢⎢S−T2S⋅(S+T)22taken opportunity+S+T2S⋅S2missed opportunity⎤⎦⎥⎥⎥.

The difference in average waiting time for these two strategies is

Δ=12SS−T2S[S2−(S+T)22]which is positive if Opportunism is better, and negative if Disregarding is better. To simplify the expression, defineβ≡T/S, where0<β<1by assumption. Then the difference in average waiting time is:Δ====12SS−T2S[S2−(S+T)22]12S(1−β)S2S[S2−S2(1+β)2/2]S8(1−β)[2−(1+β)2][β3+β2−3β+1]S

The Verdict

Answer: it depends on how quickly you walk.

In fact, the difference in waiting time varies depending on β, the fraction of the cycle time you take to cross the street.

\( \Delta = [\beta^3 + \beta^2 - 3\beta + 1]S \)

The Disregarder and Opportunist are equally efficient when this quantity is zero; that is, when β=2√−1≈41%. For shorter walking times, Opportunism is better. For longer walking times, Disregarding is better.

Intuitively, this occurs because the Opportunist can control the size of the window of opportunity by walking faster. In contrast, any advantage the Disregarder gets from walking faster is cancelled by the additional time spent waiting for the cycle to end.

This surprising result has an interesting consequence: Suppose two people walk at the same speed. One of them has to cross the street in one direction, the other has to cross in two directions. Who will take longer, on average? The answer, assuming they don't jaywalk, is that it depends on what their shared walking speed is.

How to cross the street

Dylan Holmes