Have you ever wondered about the distinctive sweeping roof shape on certain buildings? These are flying eaves (飞檐 in Chinese; 추녀, chunyeo in Korean). They are not only supremely beautiful, they also serve a key functional purpose: when the eaves are upturned, they can welcome in more sunlight while still shielding from overhead rain. This additional sunlight helps dry out wooden homes after a rainstorm and hence prevent mold and rot.

I was interested in studying the shape of these eaves and modeling their rain-protecting and light-welcoming properties.  In this article, I present a simple mathematical model that shows how these properties change depending on roof shape.

The sun on the sloping roof

For simplicity, we will consider a two-dimensional rectangular house consisting of two walls, a floor, and a ceiling. The house is aligned with the sun, so that one wall lies to the east and the other lies to the west.

Let us also assume that the sun is infinitely far away. This allows us to model the sun's rays as perfectly parallel, and chart the sun's position throughout the day using a single angle measure \(\theta\). We can say that at 0° is daybreak, when the sun appears on the horizon; 90° is high noon, when it is directly overhead; and 180° is nightfall, when the it reaches the opposite horizon.

A rectangular house in a two-dimensional world. As the angle of the sun changes, the shadow of the house changes.

Note that in the figure, I have made the unusual choice to represent East as leftward. This unusual choice means that the sun will move from left to right throughout the course of the day, which I find convenient to visualize. The figure therefore depicts some time in the morning.

Next, let us add flying eaves to the roof.  We can model an eave as a curve in the plane, say a piecewise linear function like this one:

The shape of the roof can be represented as a function with Cartesian coordinates—in this case, a piecewise linear function. The scale in this cartoon has been exaggerated to make the roof easier to see.

The rooftop contour can in general be any continuous curve, but to ensure that the eaves properly "fly" upward, we should require the contour to be a convex, increasing function. This prevents the roof from bending back onto itself, forming strange peaks, or sloping downward. The roof in the figure is a nice choice of convex, increasing function.

The umbrella equation

To calculate the effect of light and shadow on this roof, we can set up a 2D coordinate system where ground level is the line \(y=0\).  Supposing the roof is a piecewise linear function with endpoint coordinates \(\langle a_i, b_i\rangle\), how does the shadow vary with time of day \(\theta\)?

Note that each junction of the piecewise-linear roof casts its own shadow on the ground, forming a right triangle. The angle of the triangle is \(\theta\)—the angle of the sun—and the width of the triangle's base is \(b_i \cot(\theta)\) by basic trigonometry.

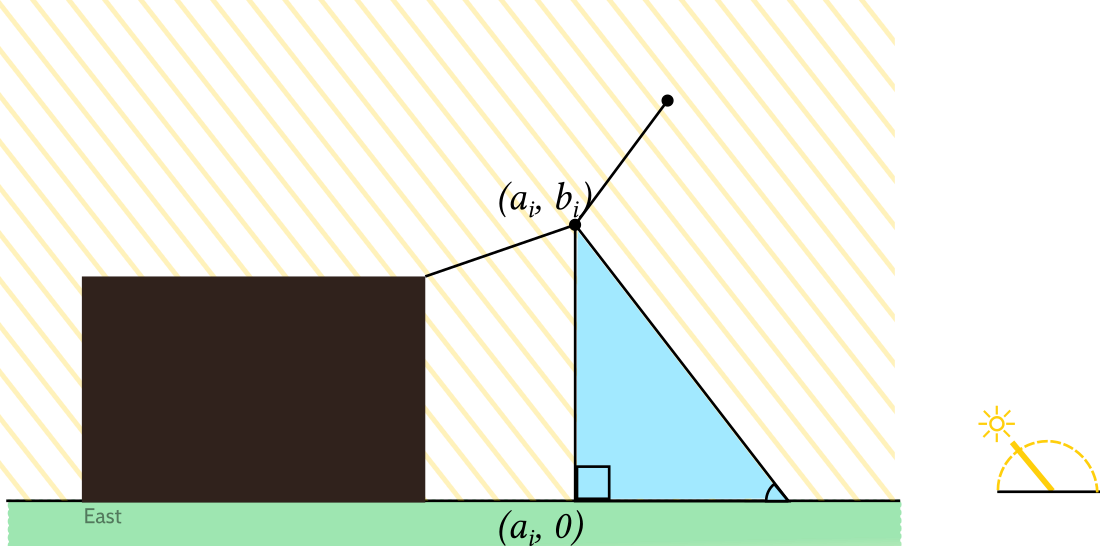
Each endpoint on the piecewise-linear roof function projects a shadow along the sunlight direction \(\theta\) onto the ground, forming a right triangle. The projected shadow of that endpoint is at position \(a_i+b_i\cot(\theta)\). Because the roof's shadow is convex, its right endpoint is the maximum of all the projected endpoints.

Putting together the shadows of all the junctions, we can see the whole shadow of the roof:

The shadow of the roof is a line segment on the ground. One endpoint is anchored on the house. The other one moves with the angle of the sun.

The figure above shows that the rightmost endpoint of the shadow is the projection of the rightmost edge of the house. This remains true throughout the morning, but in the afternoon—when shadows are cast toward the left—the rightmost end of the roof's shadow can be the projection of other endpoints instead:

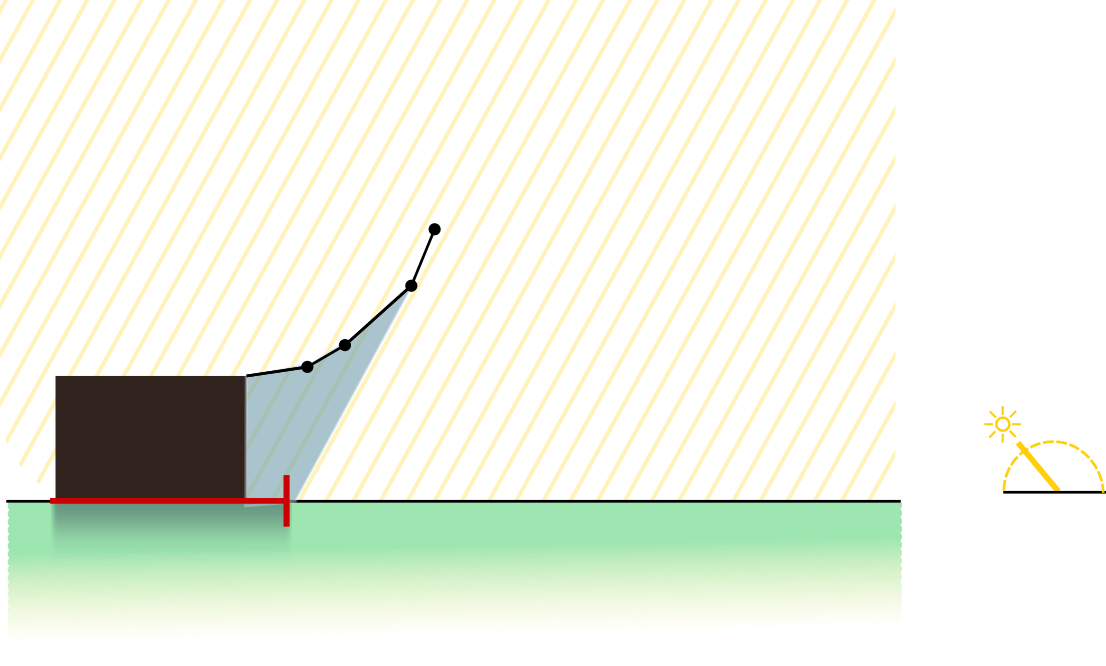
For a piecewise-linear roof, the end of the roof's shadow is always the projection of one of the roof's junctions. In the morning, it is always the projection of the rightmost junction. In the afternoon, when light enters under the eaves, it will be the projection of other junctions.

Look at the figure above. You can visualize the qualitative behavior of the shadow as it changes throughout the course of the day:

  • At daybreak, the shadow stretches westward into infinity.
  • The shadow shortens until noon, when it lies directly under the roof.
  • Starting in the afternoon, the light begins to reach the area beneath the eaves for the first time.
  • As the sunlight reaches beneath the eaves, the boundary between light and shadow is a line segment. That line is parallel to the sun's rays and passes through one of the roof's endpoints.
  • Because the curve is convex and increasing, this "terminator" line segment actually transits through each of the roof's endpoints in reverse order, from right to left.  It starts at the rightmost endpoint. It transitions between two consecutive endpoints just when the angle of the sun matches the slope of the roof segment between them.
  • At some point in the evening, the sunlight finally reaches the western foundation of the house.  The light will begin to climb the walls of the house, until it illuminates the entire western wall and roof. They will remain entirely illuminated until sunset.

We know that whatever the piecewise-linear shape of the roof, the rightmost edge of the roof's shadow will be the rightmost projection of its individual segments. Using trigonometry, we can express this using the following formula, which I call the umbrella equation:

Umbrella equation (piecewise-linear). For a piecewise linear increasing roof with endpoint coordinates \(\langle a_i, b_i\rangle\), the shadow is a line segment on the ground with one moving endpoint \(\langle \alpha(\theta), 0\rangle\). That endpoint sweeps out a position given by: $$\alpha(\theta) = \max_i \left[a_i + b_i \cot(\theta)\right]$$

In fact, the same result holds if we generalize from piecewise-linear increasing functions to any convex increasing curve:

Umbrella equation (general form). For any convex increasing roof shape with coordinates \(\langle u, f(u)\rangle\), the shadow is a line segment whose moving endpoint sweeps out a curve \(\langle \alpha(\theta), 0\rangle\) given by: $$\alpha(\theta) = \sup_u \left[u + f(u) \cot(\theta)\right]$$

The interplay of light and rain

We now understand how a roof with a given shape lets in light throughout the day; it is governed by the umbrella equation. How about the rain?

If the day is not so windy, then rain falls vertically onto the roof (the same as the sun's rays at noontime.)  The shadow of the rain extends exactly as far as the rightmost part of the roof, regardless of time of day.

Without wind, the rain falls vertically downward, just as the rays of sun at noon. The shadow of the rain extends exactly as far right as the rightmost part of the roof, regardless of time of day.

How the height of the roof matters. We can learn something by contrasting how the sun and the rain fall onto the roof.  For one thing, a higher roof allows more sunlight to come in, but does not affect the rain at all.  In an extreme case, a roof with extremely high eaves would shelter everything under it from the rain, while only minimally affecting the amount of sunlight in the afternoon. (Alas, in the morning, such a tall eave would leave the entire west side of the house in shadow.)