If there's a unique two-step path between every pair of nodes in a directed graph, then every node has \(k\) neighbors and the graph has \(k\) loops, where \(k^2\) is the number of nodes in the graph.

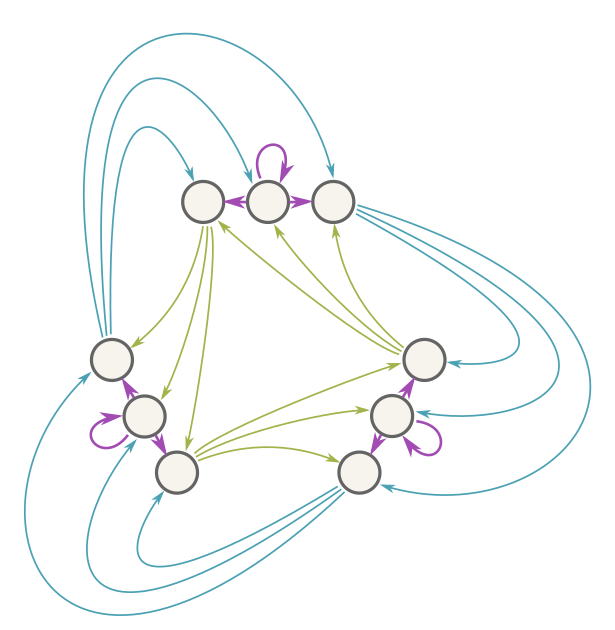
A graph where there's exactly one two-step path from any node to any node. In any graph like this, the number of nodes must be the square of the number of loops.

Astonishingly, you can prove this result using the machinery of linear algebra. You represent the graph as a matrix \(M\) whose \((i,j)\) entry is one if nodes i and j are neighbors, or 0 otherwise. The sum of the diagonal entries (the trace of the matrix) tells you the number of loops. The trace is also equal to the sum of the generalized eigenvalues, counting repetitions, so you can count loops in a graph by finding all the eigenvalues of the corresponding matrix.

The property about paths translates into the matrix equation \(M^2 = J\), where \(J\) is a matrix of all ones. (The r-th power of a matrix counts r-step paths between nodes.) This matrix \(J\) has a number of special properties—multiplying a matrix by \(J\) computes its row/column totals (i.e. the number of neighbors for a graph!), multiplying \(J\) by \(J\) produces a scalar multiple of \(J\), and \(J\) zeroes-out any vector whose entries sum to zero; this is an \(n-1\) dimensional subspace. The property that \(M^2=J\), along with special properties of \(J\), allows you to conclude that higher powers of \(M\) are all just multiples of \(J\); in particular, examining \(M^3=MJ=JM\) reveals that every node in the graph has the same number of neighbors \(k\). So \(M^3 = kJ\). (And \(k^2 = n\) because \(k^2\) is the number of two-step paths, which lead uniquely to each node in the graph.)  Notice that because of this neighbor property, \(M\) sends a column vector of all ones to a column vector of all k's, so \(M\) has an eigenvalue \(k\). Based on the powers of \(M\), \(M\) furthermore has \((n-1)\) generalized eigenvectors with eigenvalue zero. There are always exactly \(n\) independent generalized eigenvalues, and we've just found all of them. Their sum is \(0+0+0+\ldots+0+k = k\), which establishes the result.

The same procedure establishes a more general result: If there's a unique r-step path between every pair of nodes in a graph, then every node has k neighbors and the graph has k loops, where \(k^r\) is the number of nodes in the graph.