How do you cut a gemstone to make it shine brightest? Can you find an ideal shape using physical principles?

Gems are usually set into a ring or other piece of jewelry so that one main face (the "crown") is visible. Light enters the gem through the crown, where it bounces off of the interior facets and/or leaks through them. The brightness of a gem is determined by how much light is reflected back out through the crown instead of leaking out. Therefore, the simple rule for achieving shiny gems is:

Reflect as much light as possible back out of the crown.

This is basically a geometry problem: using mirrors and glass, you could design a triangular retroreflector that bounced light around in exactly this way. In 2D, you would make an isosceles triangle where the base side (the crown) is clear glass, and the other two sides are mirrored. By choosing good angles for the triangle, you could ensure that all light entering straight into the crown would bounce off the two mirrored sides and emerge back out. Problem solved.

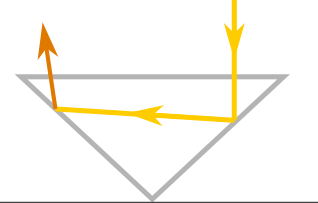
A triangular retroreflector, with two mirrored legs, can reflect all incoming light back out of the crown.

For gemstones, however, there is also a materials problem: even polished gemstones are translucent, not mirrored. So, light entering the crown will tend to leak out of the bottom facets instead of bouncing---the surface behaves more like glass than a mirror. However, there is a solution: if light strikes the gemstone from an appropriately shallow angle, it will bounce perfectly instead of leaking through. This phenomenon is total internal reflection: when light that hits a surface at a shallow angle, the surface behaves like an essentially perfect mirror. (When you dive into a swimming pool and look up at the surface of the water, total internal reflection explains why the surface forms a perfect silvery mirror except for a small circular window.)

Every material has its own critical angle, which is determined by the material's refractive index.

A laser hitting the surface of the water at a shallow angle will reflect off of it like a perfect mirror, instead of shining through. Image from http://sites.fas.harvard.edu/~scidemos/LightOptics/FishTankTIR/FishTankTIR.html

Returning to our triangular model, the material's critical angle will determine how steep we should make the sides of the gemstone. We want to make it steep enough so that the walls of the gem become mirrored and all the light entering straight into the crown will be reflected out. We are looking for a design parameter: what angle to make our triangle. Gemologists refer to this design parameter as the pavillion angle, labeled as \alpha in the figure below. We have four constraints on \alpha altogether: two geometric constraints and two material constraints.

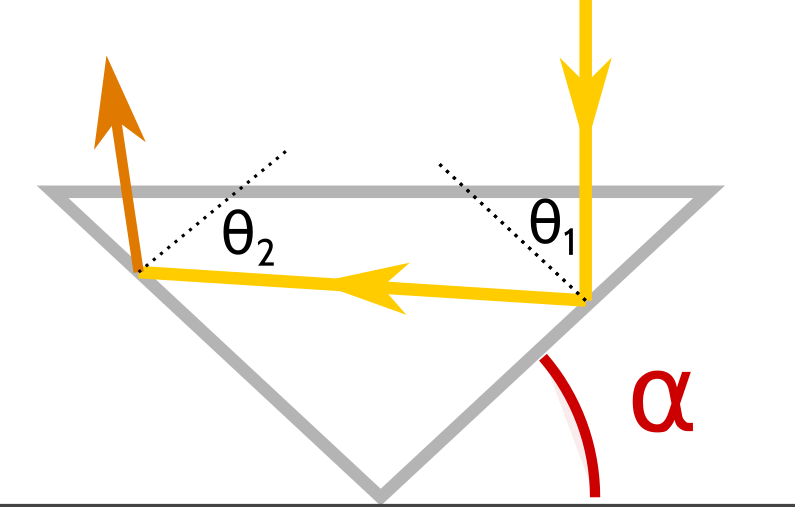
A triangular gem. The choice of pavillion angle \alpha controls the reflection angles \theta_1 and \theta_2. They must be shallow enough to enable total internal reflection in our chosen material. 
  1. The angles \(\theta_1\) and \(\theta_2\) represent reflections, so they must lie between 0 and 90 degrees.
  2. By triangle geometry, \(\theta_1=\alpha\), and \(\theta_2 = 180^\circ -3\alpha\).
  3. In order for the first bounce to behave like a mirror, \(\theta_1\) must exceed the material's critical angle.
  4. In order for the second bounce to behave like a mirror, \(\theta_2\) must exceed the material's critical angle.

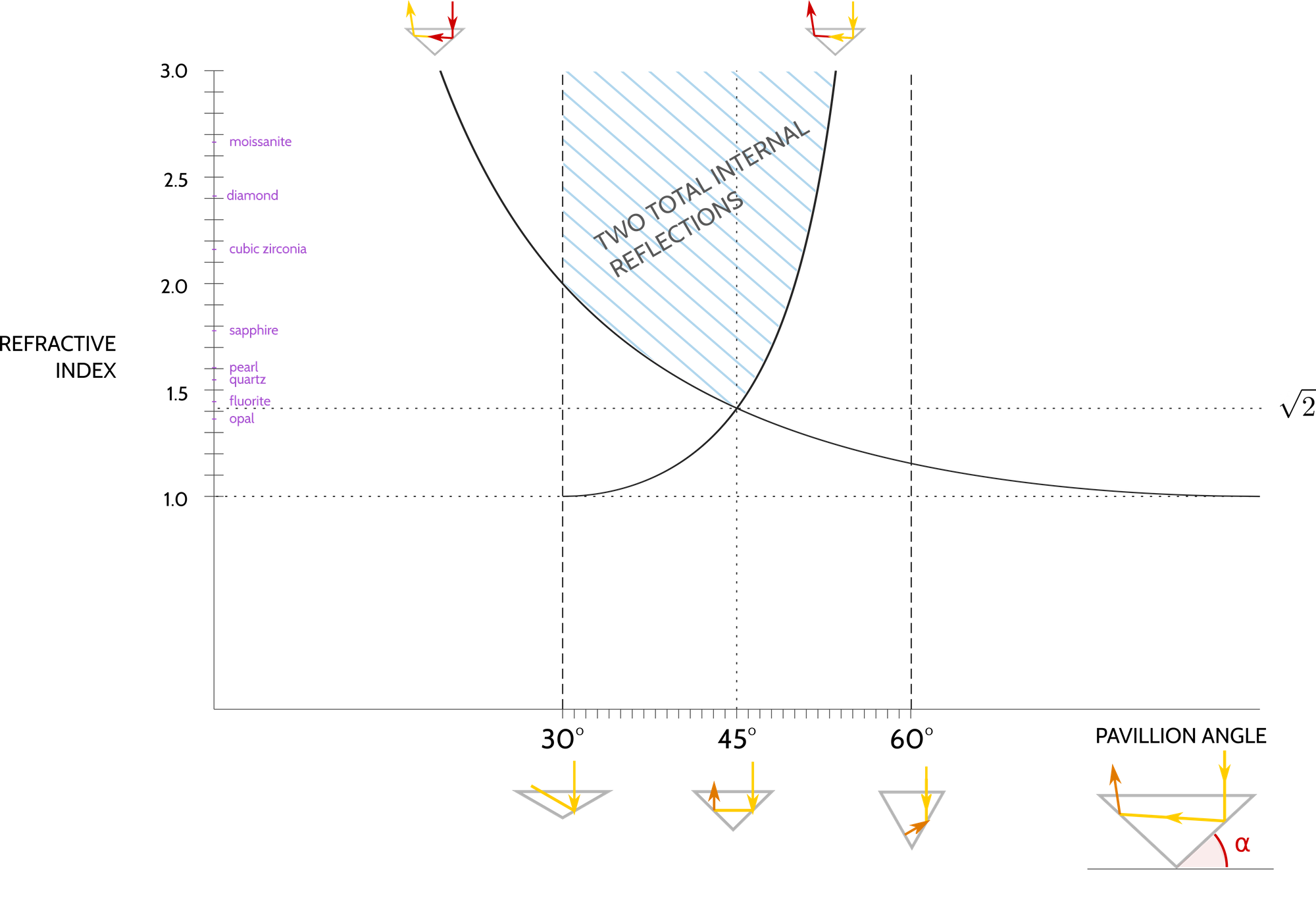
These four constraints, along with the definition of critical angle \(\theta_c = \arcsin(1/n)\) in terms of refractive index n, enable us to find the acceptable range of angles for making our shiny gemstone.

In the following graph, I have depicted the four constraints and their range of solutions:

A gemstone becomes a perfect mirror when its underside is cut into an appropriate triangular shape. As shown in this graph, the range of allowed pavillion angles (horizontal axis) depends on the refractive index of the gemstone material (vertical axis). 

Fun Applications

In short, we have learned—to first approximation—that you make a gemstone shine brightest by making it into a retroreflector with two internal rotations. You can dream up some interesting consequences of this fact, a few of which I enumerate below:

  • Gems are like other retroreflectors. Gems work by using mirrored surfaces to send incoming light right back out, the same principle as eyeshine in cats and other animals, and those bright retroreflectors on highways.
  • Miscut gems become windows. If you cut the gem at the wrong angle, the bottom facets will leak light instead of reflecting the light back up. Gemologists refer to this unfortunate event as windowing the gem. We now understand the physics behind it: instead of becoming total internal reflectors, the facets of a miscut gem remain translucent like windows.
  • You can't make gems out of certain materials. Our recipe is for making a gemstone using two total internal reflections. If a material's refractive index is below \(\sqrt{2}\approx 1.41\), you can't achieve those two internal reflections.
  • A bigger index means a wider range. Materials with greater refractive indices have more flexible ranges of pavillion angle.
  • You can quench fire with water. The shape of a gem is tailored to the refractive index of the material and also, implicitly, the refractive index of air. If you put a loose gem into water, its facets stop behaving like perfect mirrors and it loses all of its sparkle.
  • Sunlight is best. In our approximation, we only imagined parallel light rays coming straight into the sun. Of course, most lighting environments have diffuse light coming in from all directions. A superb example of parallel light is sunlight; hence gems will look their best when you're looking straight into the crown, and the sun's rays shine directly into the crown as well.
  • You can make cones, too. In 3D, instead of making the pavillion out of triangular facets, you could simply lathe the gem into a cone of the appropriate angle. This would achieve the total internal reflection just as well as discrete facets. It wouldn't have sparkling facets, but I expect it would have its own smoothly luminous beauty.
  • You can't see through a gem. Here's one way to confirm that gems use total internal reflection: you can't see through it when you're looking through the crown! This is most obvious on a large, loose, translucent gem: hold the gem up to a colorful surface and look through the crown. You won't be able to see the colorful surface through the gem.